EXPRESIÓN REGULAR QUE REPRESENTA EL MISMO LENGUAJE QUE UN AUTÓMATA FINITO
Cojamos el siguiente autómata finito para el alfabeto
S = { x, y, z }: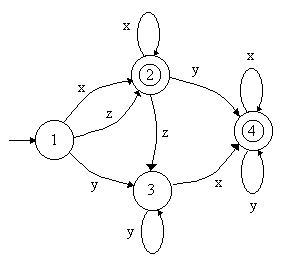
En primer lugar vemos que el diagrama tiene dos estados de aceptación, por tanto, lo primero que hay que hacer es una copia del diagrama para cada uno de ellos. Cojamos el diagrama para el que el estado de aceptación es el 4.
Primero vamos a hacer la unión de
las transiciones que tienen el mismo origen y destino (que puede ser el mismo). En nuestro
diagrama tenemos dos casos:
+ Entran dos arcos desde el estado 1 al 2 con etiquetas "x" y "z". Se sustituyen por un arco
etiquetado con (x
+ En el estado 4 entran y salen del mismo dos arcos con etiquetas "x" y "z". Se sustituyen por un arco que entra y sale del estado 4 etiquetado con (x u y).
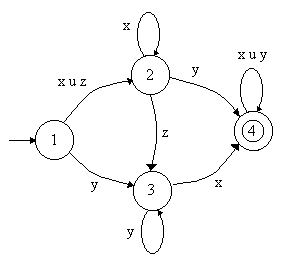
Para empezar a reducir vamos a elegir el
estado 2. Para poder eliminarlo tenemos que sustituirlo por dos transiciones; una hacia el
estado 3 y otra al estado 4:
+ Para la transición al estado 3 la expresión será la
concatenación del arco incidente, la estrella de Kleene del arco que empieza y acaba
en el estado 2 y el arco que sale hacia el estado 3:
(x
u z) o x* o z. + Para la transición al estado 4 es igual pero con el arco que sale hacia este:(x
u z) o x* o y.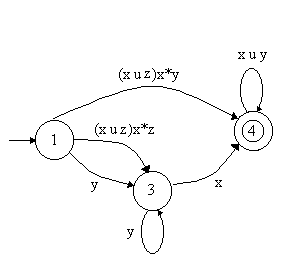
Ahora volvemos a empezar, es decir, hacemos
la unión de todas las transiciones que tienen el mismo origen y destino. Ahora solo se
da este caso en las transiciones del estado 1 al 3.
y
u [(x u z) o x* o z ]. Ahora eliminamos el estado 3 haciendo la
concatenación correspondiente. En este caso solo hay una transición al estado
4:
.
( y
u [(x u z) o x* o z ] ) o y* o x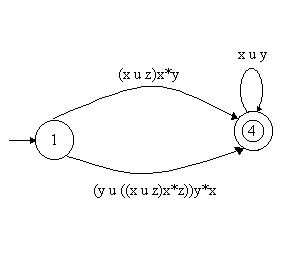
En estos momentos tenemos un diagrama con dos estados (es lo que estabamos buscando). Aplicando otra vez la unión de transiciones desde el estado 1 al 4 y concatenanado con la estrella de Kleene de las transiciones del estado 4 al mismo, la expresión que corresponde a esta copia del diagrama para el estado de aceptación 4 será:
[ ( ( y u [(x u z) o x* o z ] ) o y* o x ) u [ (x u z) o x* o y ] ] o (x u y)En la otra copia del autómata para el estado de aceptación en el estado 2. Como podemos ver, podemos eliminar los estados 3 y 4 pues no influyen en las cadenas que puede aceptar. Así nos queda un diagrama de dos estados, cuya expresión equivalente es la unión de las transiciones x e y concatenadas con la estrella de Kleene de la transición que entra y sale en el estado 2 quedando la expresión:
(x
u z) o x*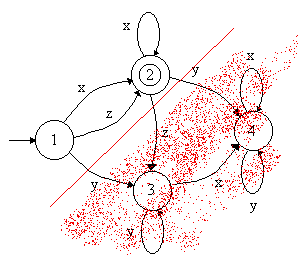
Ahora procedemos a la unión de las expresiones resultantes para cada copia del autómata con un estado de aceptación, siendo esta la expresión equivalente al autómata original:
[
[ ( ( y u [(x u z) o x* o z ] ) o y* o x ) u [ (x u z) o x* o y ] ] o (x u y) ]u
( (x u z) o x* )
Denotar que si en el diagrama original el estado inicial hubiese sido de aceptación, el diagrama resultante de ir reduciendo el anterior, habría sido de sólo un estado).
Nota: En los diagramas se ha omitido el símbolo de concatenación para claridad.
© 1999 Roberto de la Fuente López. Todos los derechos reservados
Fecha de actualización: 15 de abril de 1999
