Sea la gramática regular para el alfabeto S = { x, y } tal que, si x=5 e y=10, representa el lenguaje de todas las cadenas que suman 20:

• Primero tenemos que convertirla en una gramática G' que genera el mismo lenguaje pero que no contiene reglas de reescritura cuyo lado derecho sea solo un terminal. Para eliminar estas reglas se sustituye por dos reglas de reescritura, una cuya parte derecha será siempre un terminal seguido de un no terminal, el cual no existía en la gramática original y la otra cuya parte izquierda es ese no terminal nuevo y la derecha es la cadena vacía.

     N® x      se sustituye por      N ® xX

  X ®l

  La gramática que nos ocupa tiene las dos últimas reglas de reescritura con un solo terminal y por lo tanto tenemos que convertirla. Para ello vamos a insertar el no terminal Apara la regla vacía; la gramática G' quedará entonces:
   
  S ® xX
  S ® yY
  X ® xY
  X ® yZ
  Y ® xZ
  Y ® yA
  Z ® xA
  A ® l
  
• S es la colección de no terminales de G'. En nuestro caso particular, los estados serán: S = { S, X, Y, Z, A }. (no confundir la S del conjunto -no terminales- con la S del elemento -símbolo de inicio de la gramática-, el cual también conviene cambiar, pero que no se ha hecho por claridad).
• i es el símbolo inicial de G’. Es decir, el estado S
• F es la colección de no terminales de G' que aparecen en el lado izquierdo de alguna regla l. En nuestro caso va a ser sólo el estado A.
  
   
  

  

• r consiste en la tripleta (P, x, Q) (de aquí que el autómata sea no determinista)para el cual G' contiene una regla de reescritura de la forma P® xQ
  

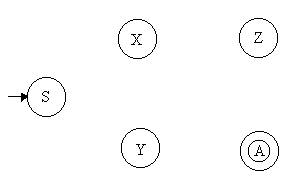
  + S ® xX : transición del estado S al X con etiqueta x
  + S ® yY: Transición del estado S al Y con etiqueta y

  

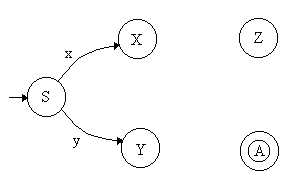
  + X ® xY : Transición del estado X al Y con etiqueta x
  + X ® yZ: Transición del estado X al Z con etiqueta y

  

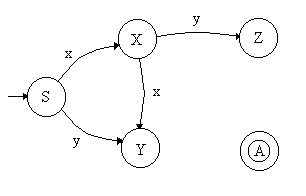
  + Y ® xZ: Transición del estado Y al Z con etiqueta x
  + Y ® yA: Transición del estado Y al A con etiqueta y
  
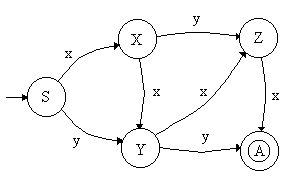
  + Z ® xA: Transición del estado Z al A con etiqueta x
  + A ® l: No hay transición definida