EJEMPLO DE AUTÓMATA FINITO
Retomemos el ejemplo anterior: El autómata que acepta los nombres de variables en un lenguaje de programación. Recordar que estos nombre debían empezar por una letra seguida de una letra o un número y tampoco admiten caracteres especiales.
1.- Diagrama de transiciones
Vista esta descripción en lenguaje natural, pasemos a describirlo en base a un diagrama de transiciones.
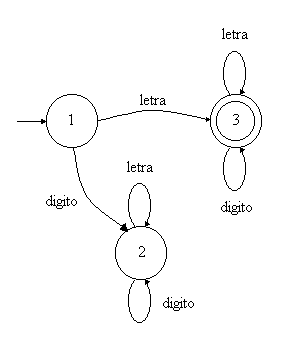
Este diagrama está totalmente definido (se verá mas adelante porque), es decir, hay transiciones desde cada uno de los estados para cada uno de los elementos posibles (letras o números). Una cadena de la forma "5aba" producirá una transición del estado 1 al 2, permaneciendo allí hasta FDC. La cadena se rechaza pues el estado 2 no es de aceptación.
Otra forma de ver que no se puede aceptar una cadena es que no haya una transición posible en el diagrama (con diagramas que no estén totalmente definidos) antes de que ocurra FDC.
Para hacer la tabla de transiciones, necesitamos tener definido totalmente el autómata (luego se verá como se completa un autómata que no esté totalmente definido).
Para nuestro ejemplo, siguiendo los pasos expuestos, nos quedará la siguiente tabla:
| LETRA | NÚMERO | FDC | |
|---|---|---|---|
| Estado 1 | 3 | 2 | error |
| Estado 2 | 2 | 2 |
|
| Estado 3 | 3 | 3 | aceptar |
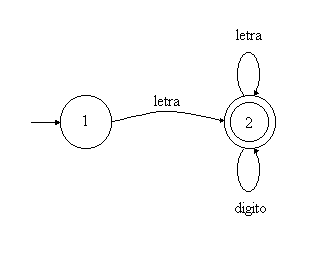
Hay que reseñar un detalle; si, por ejemplo, en estado 2 no existiera, la transición del estado 1 con un número sería error. El diagrama (que ya no estaría totalmente definido) y la tabla correspondiente quedarían entonces:
| LETRA | NÚMERO | FDC | |
|---|---|---|---|
| Estado 1 | 2 | error | error |
| Estado 2 | 2 | 2 | aceptar |
Para realizar un programa, podemos basarnos en la definición del autómata con el diagrama o con la tabla. Sin embargo, el programa que se realice a partir de la tabla será más eficiente en cuanto a tiempo de ejecución, sobre todo si hay muchos estados (si hay muchos estados, puede que no haya suficiente memoria física para la tabla). Los programas quedarían, para el primer ejemplo expuesto:
|
resultado:=true; estado:=1; simbolo:=primer elemento de la cadena; repeat numero:estado:=2; 2:case simbolo of numero:estado:=2 3:case simbolo of numero:estado:=3 simbolo:=siguiente elemento de la cadena if resutado then print "aceptada" else print "no aceptada" |
inicializa el indicador para el resultado final inicializa el estado al inicial simbolo:=primer elemento de la cadena inicializa simbolo al primero de la cadena dependiendo de si hay mas estados que simbolos o viceversa, los bucles se pueden intercambiar |
Para el caso del programa basado en la tabla de transiciones:
|
estado:=1 simbolo:=primer elemento de la cadena; repeat simbolo:=siguiente elemento de la cadena if estado=aceptar then print "cadena aceptada" |
En el segundo caso el programa valdría para cualquier autómata con tres estados y dos símbolos aparte de FDC con solo cambiar los datos de la tabla
© 1999 Roberto de la Fuente López. Todos los derechos reservados
Fecha de actualización: 14 de abril de 1999
