Dado un alfabeto, S, vamos a considerar todas las cadenas de longitud finita (incluyendo la vacía), a partir de este alfabeto y lo vamos a designar con S^*(no confundirlo con el conjunto potencia del alfabeto, por ejemplo, en el alfabeto {a,b}, S^* será { l, a, b, aa, bb, ab, ba, aaa, aab,...} y P(S)={l, a, b, ab}). Un subconjunto de S^* se llama lenguaje (varios subconjuntos denotarán distintos lenguajes).

     Si M es un autómata finito determinista (S,S, d,i ,F), la colección de cadenas que acepta constituye un lenguaje con respecto al alfabeto S; Este lenguaje lo representamos con L(M) que se lee "el lenguaje que acepta M". L(M) es la colección de TODAS las cadenas que acepta M (ni más ni menos). El lenguaje que es aceptado por un autómata finito se llama lenguaje regular.

• La colección de todas las cadenas de longitud finita de un alfabeto ( S^* )

• La colección de ninguna cadena, conocido como lenguaje vacío y se representa con Æ (hay que diferenciar el lenguaje con la cadena vacía { l} y el lenguaje que no tiene cadenas {Æ} El primero tiene una cadena y el segundo no tiene ninguna).

  

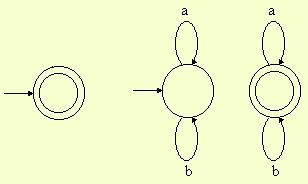
  cadena vacía                                     lenguaje vacío

     Como estamos hablando de conjuntos de cadenas, podemos decir que S^* es el conjunto universal, y {Æ } su complementario. Como los dos son lenguajes regulares, entonces podemos generalizar a cualquier lenguaje regular y su complementario, que son regulares también.

COROLARIO.- Para cualquier lenguaje regular aceptado por un autómata finito determinista L(M), existe el autómata finito determinista L(M') que acepta el lenguaje complementario con respecto al universal (L(M') = S^* - L(M)).

     Sea Wⁿ, donde W es una cadena de S^* y n es un entero no negativo. Wⁿ es la forma abreviada para representar una cadena de n copias del patrón W (si S={x,y}, entonces (xy)³=xyxyxy o y⁰=l ).